Линейные операторы в евклидовом пространстве. Операторы проекции Операторы проектирования y z 0
Бра- и кет- векторы Дирака замечательны тем, что с помощью них можно записать различные типы произведений.
Произведение бра-вектора на кет- вектор называется скалярным произведением или внутренним произведением. По сути это стандартное матричное произведение по правилу «строка на столбец». Результатом его есть комплексное число.
Произведение кет-вектора на другой кет-вектор дает уже не число, а другой кет-вектор. Он тоже представляется вектор-столбцом, но с количеством компонент равном произведению размерностей исходных векторов. Такое произведение называется тензорным произведением или произведением Кронекера.
Аналогично и для произведения двух бра-векторов. Получим большую вектор-строку.
Последним остается вариант с перемножением кет-вектора на бра-вектор. То есть необходимо перемножить столбец на строку. Такое произведение также называется тензорным или внешним произведением. В его результате получается матрица, то есть оператор.
Рассмотрим пример использования таких операторов.
Возьмем какой-нибудь произвольный эрмитов оператор А. Согласно постулатам ему соответствует какая-то наблюдаемая величина. Собственные векторы эрмитового оператора формируют базис. Наиболее общий вектор состояния можно разложить по этому базису. То есть представить суммой базисных векторов с определенными комплексными коэффициентами. Данный факт известен как принцип суперпозиции. Перепишем выражение через знак суммы.
Но коэффициенты в разложении вектора по базисным есть амплитуды вероятности, то есть скалярное произведение вектора состояния с соответствующим базисным вектором. Запишем эту амплитуду справа от вектора. Выражение под знаком суммы можно рассматривать как умножение кет-вектора на комплексное число – амплитуду вероятности. С другой стороны его можно рассматривать как произведение матрицы, полученной умножением кет-вектора на бра-вектор, и исходного кет-вектора. Кет-вектор можно вынести из под знака суммы за скобку. Справа и слева знака равенства окажется один и тот же вектор пси. Это значит, что вся сумма ничего не делает с вектором и соответственно равна единичной матрице.
Данная формула сама по себе очень полезна при манипулировании выражениями с произведениями бра- и кет- векторов. Ведь единицу можно вставить в любое место произведения.
Посмотрим что же из себя представляют матрицы, входящие в сумму и получаемые тензорным произведением базисного кет-вектора со своим эрмитовым сопряжением. Опять же для наглядности проведем аналогию с обычными векторами в трехмерном пространстве.
Выберем единичные базисные векторы ex ey и ez, совпадающие по направлению с осями координат. Тензорное произведение вектора ex на свое сопряжение будет представляться следующей матрицей. Возьмем произвольный вектор v. Что же будет при умножении этой матрицы на вектор? Данная матрица просто обнулила все компоненты вектора кроме х. В итоге получился вектор, направленный вдоль оси х, то есть проекция исходного вектора на базисный вектор ex. Выходит наша матрица есть не что иное как оператор проекции.
Оставшиеся два оператора проекции на базисные векторы ey и ez представляются похожими матрицами и выполняют аналогичную функцию – обнуляют все кроме одной компоненты вектора.
Что же получится при суммировании операторов проекции? Сложим например операторы Px и Py. Такая матрица будет обнулять только z-компоненту вектора. Итоговый вектор всегда будет лежать в плоскости x-y. То есть мы имеем оператор проекции на плоскость x-y.
Теперь понятно почему сумма всех операторов проекции на базисные векторы равна единичной матрице. В нашем примере мы получим проекцию трехмерного вектора на само трехмерное пространство. Единичная матрица по-сути и есть проектор вектора самого на себя.
Получается задание оператора проекции эквивалентно заданию подпространства исходного пространства. В рассматриваемом случае трехмерного евклидового пространства это может быть одномерная линия, задаваемая одним вектором или двумерная плоскость, задаваемая парой векторов.
Возвращаясь к квантовой механике с ее векторами состояния в Гильбертовом пространстве, можно сказать что операторы проекции задают подпространство и проецируют вектор состояния в это Гильбертово подпространство.
Приведем основные свойства операторов проекции.
- Последовательное применение одного и того же оператора проекции эквивалентно одному оператору проекции. Обычно данное свойство записывают как P 2 =P. Действительно, если первый оператор спроецировал вектор в подпространство, то второй уже ничего с ним не сделает. Вектор ведь уже будет находиться в этом подпространстве.
- Операторы проекции являются эрмитовыми операторами, соответственно в квантовой механике им соответствуют наблюдаемые величины.
- Собственные значения операторов проекции любой размерности это только числа единица и ноль. Находится вектор в подпространстве или не находится. Из-за такой бинарности, описываемую оператором проекции наблюдаемою величину можно сформулировать в виде вопроса, ответом на который будет «да» или «нет». Например, направлен ли спин первого электрона в синглетном состоянии вверх по оси z? Такому вопросу можно поставить в соответствие оператор проекции. Квантовая механика позволяет посчитать вероятности для ответа «да» и для ответа «нет».
В дальнейшем мы еще будем говорить об операторах проекции.
Пусть линейный оператор А действует в евклидовом пространстве E n и преобразует это пространство само в себя.
Введем определение : оператор А * назовем сопряженным оператору А , если для любых двух векторов x,y из Е n выполняется равенство скалярный произведений вида:
(Ax,y ) = (x,A * y )
Еще определение : линейный оператор называется самосопряженным, если он равен своему сопряженному оператору, т. е. справедливо равенство:
(Ax,y ) = (x,Ay )
или, в частности (Ax,x ) = (x,Ax ).
Самосопряженный оператор обладает некоторыми свойствами. Упомянем некоторые из них:
Собственные числа самосопряженного оператора - вещественны (без доказательства);
Собственные векторы самосопряженного оператора ортогональны. Действительно, если x 1 и x 2 – собственные векторы, а 1 и 2 – их собственные числа, то: Ax 1 = 1 x ; Ax 2 = 2 x ; (Ax 1 ,x 2 ) = (x 1 ,Ax 2 ), или 1 (x 1 ,x 2 ) = 2 (x 1 ,x 2 ). Поскольку 1 и 2 различны, то отсюда (x 1 ,x 2 ) = 0, что и требовалось доказать.
В евклидовом пространстве существует ортонормированный базис из собственных векторов самосопряженного оператора А . Т. е. матрицу самосопряженного оператора всегда можно привести к диагональному виду в некотором ортонормированном базисе, составленном из собственных векторов самосопряженного оператора.
Еще одно определение : назовем самосопряженный оператор, действующий в евклидовом пространстве симметричным оператором. Рассмотрим матрицу симметричного оператора. Докажем утверждение: чтобы оператор был симметричным, необходимо и достаточно, чтобы в ортонормированном базисе его матрица была бы симметричной.
Пусть А – симметричный оператор, т. е.:
(Ax,y ) = (x,Ay )
Если А – матрица оператора А, а x и y – некоторые векторы, то запишем:
 координаты
x
и y
в некотором ортонормированном базисе
координаты
x
и y
в некотором ортонормированном базисе
Тогда: (x,y ) = X T Y = Y T X и имеем (Ax,y ) = (AX) T Y = X T A T Y
(x,Ay ) = X T (AY) = X T AY,
т.е. X T A T Y = X T AY. При произвольных матрицах-столбцах X,Y это равенство возможно только при А Т = А, а это означает, что матрица А – симметричная.
Рассмотрим некоторые примеры линейных операторов
Оператор проектирования. Пусть требуется найти матрицу линейного оператора, осуществляющего проектирование трехмерного пространства на координатную ось е 1 в базисе е 1 , е 2 , е 3 . Матрица линейного оператора – это матрица, в столбцах которой должны стоять образы базисных векторов е 1 = (1,0,0), е 2 = (0,1,0), е 3 = (0,0,1). Эти образы, очевидно, есть: Ае 1 = (1,0,0)
Ае 2 = (0,0,0)
Ае 3 = (0,0,0)
Следовательно, в
базисе е
1
,
е
2
,
е
3
матрица
искомого линейного оператора будет
иметь вид:

Найдем ядро этого оператора. Согласно определению ядро – это множество векторов х , для которых АХ = 0. Или


Т. е. ядро оператора составляет множество векторов, лежащих в плоскости е 1 , е 2 . Размерность ядра равна n – rangA = 2.
Множество образов этого оператора – это, очевидно, множество векторов, коллинеарных е 1 . Размерность пространства образов равна рангу линейного оператора и равна 1 , что меньше размерности пространства прообразов. Т. е. оператор А – вырожденный. Матрица А тоже вырождена.
Еще пример : найти матрицу линейного оператора, осуществляющего в пространстве V 3 (базис i , j , k ) линейное преобразование – симметрию относительно начала координат.
Имеем: Ai = -i
Т. е. искомая матрица

Рассмотрим линейное преобразование – симметрию относительно плоскости y = x .

Aj = i (1,0,0)
Ak = k (0,0,1)
Матрица оператора будет:

 Еще пример –
уже знакомая матрица, связывающая
координаты вектора при повороте осей
координат. Назовем оператор, осуществляющий
поворот осей координат, - оператор
поворота. Допустим, осуществляется
поворот на угол :
Еще пример –
уже знакомая матрица, связывающая
координаты вектора при повороте осей
координат. Назовем оператор, осуществляющий
поворот осей координат, - оператор
поворота. Допустим, осуществляется
поворот на угол :
Ai ’ = cosi + sinj
Aj ’ = -sini + cosj
Матрица оператора поворота:

Ai ‘ Aj ‘
Вспомним формулы преобразования координат точки при смене базиса – замена координат на плоскости при смене базиса:

Э ти
формулы можно рассматривать двояко.
Ранее мы рассматривали эти формулы так,
что точка стоит на месте, поворачивается
координатная система. Но можно
рассматривать и так, что координатная
система остается прежней, а перемещается
точка из положения М *
в положение М. Координаты точки М и М*
определены в той же координатной системе.
ти
формулы можно рассматривать двояко.
Ранее мы рассматривали эти формулы так,
что точка стоит на месте, поворачивается
координатная система. Но можно
рассматривать и так, что координатная
система остается прежней, а перемещается
точка из положения М *
в положение М. Координаты точки М и М*
определены в той же координатной системе.
В се
сказанное позволяет подойти к следующей
задаче, которую приходится решать
программистам, занимающимся графикой
на ЭВМ. Пусть необходимо на экране ЭВМ
осуществить поворот некоторой плоской
фигуры (например треугольника) относительно
точки О’ с координатами (a,b)
на некоторый угол .
Поворот координат описывается формулами:
се
сказанное позволяет подойти к следующей
задаче, которую приходится решать
программистам, занимающимся графикой
на ЭВМ. Пусть необходимо на экране ЭВМ
осуществить поворот некоторой плоской
фигуры (например треугольника) относительно
точки О’ с координатами (a,b)
на некоторый угол .
Поворот координат описывается формулами:

Параллельный перенос обеспечивает соотношения:

Для того, чтобы решить такую задачу, обычно применяют искусственный прием: вводят так зазываемые “однородные” координаты точки на плоскости XOY: (x, y, 1). Тогда матрица, осуществляющая параллельный перенос, может быть записана:

Действительно:

А матрица поворота:

Рассматриваемая задача может быть решена в три шага:
1 й шаг: параллельный перенос на вектор А(-а, -b) для совмещения центра поворота с началом координат:

2 й шаг: поворот на угол :

3 й шаг: параллельный перенос на вектор А(а, b) для возвращения центра поворота в прежнее положение:

Искомое линейное преобразование в матричном виде будет выглядеть:
 (**)
(**)

1. Операторы проектирования и идемпотенты кольца
Пусть векторное пространство V равно прямой сумме подпространств W и L: . По определению прямой суммы это означает, что каждый вектор vV однозначно представим в виде v=w+l, wW. lL.
Определение 1. Если, так что v=w+l, то отображение, сопоставляющая каждому вектору vV его компоненту (проекцию) wW, называется проектором пространства V на пространство W. называют также оператором проектирования, или проекционным оператором.
Очевидно, если wW, то (w)=w. Отсюда следует, что обладает следующим замечательным свойством 2 =Р.
Определение 2. Элемент е кольца K называется идемпотентом (т. е. подобным единице), если е 2 =е.
В кольце целых чисел есть всего два идемпотента: 1 и 0. Иное дело в кольце матриц. Например, матрицы, - идемпотенты. Матрицы операторов проектирования также идемпотенты. Соответствующие им операторы называются идемпотентными операторами.
Рассмотрим теперь прямую сумму n подпространств пространства V:
Тогда аналогично случаю прямой суммы двух подпространств можем получить n операторов проектирования, …, . Они обладают свойством ==0 при ij.
Определение 3. Идемпотенты e i и e j (ij) называются ортогональными, если e i e j = e j e i =0. Следовательно, и - ортогональные идемпотенты.
Из того, что IV=V, и из правила сложения линейных операторов следует, что
Это разложение называется разложением единицы в сумму идемпотентов.
Определение 4. Идемпотент е называется минимальным, если его нельзя представить в виде суммы идемпотентов, отличных от е и 0.
2. Каноническое разложение представления
Определение 5. Каноническим разложением представления Т(g) называется его разложение вида Т(g)=n 1 T 1 (g)+ n 2 T 2 (g)+…+ n t T t (g), в котором эквивалентные неприводимые представления Т i (g) объединены вместе, причем n i - кратность вхождения неприводимого представления T i (g) в разложение T(g).
Теорема 1. Каноническое разложение представления определяется с помощью проекционного оператора вида

I=1, 2, …, t, (31)
где |G| - порядок группы G; m i - степени представлений T i (g), где i=1, 2, …, t; i (g), i=1, 2, …, t - характеры неприводимых представлений T i (g). При этом m i определяется по формуле
3. Проекционные операторы, связанные с матрицами неприводимых представлений групп
С помощью формул (31) можно получить только каноническое разложение представления. В общем случае, надо воспользоваться матрицами неприводимых представлений, которые позволяют построить соответствующие операторы проектирования.
Теорема 2. Пусть - матричные элементы неприводимого представления T r (g) группы G. Оператор вида

является оператором проектирования и называется оператором Вигнера. В выражении (33) m r - размерность представления T r (g).
4. Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Обозначим через М модуль, связанный с представлением Т. Пусть неприводимым представлениям Т 1 , Т 2 , …, Т t из канонического разложения представления согласно методу, описанному ранее (см. § 4), соответствуют неприводимые подмодули М 1 , М 2 , …, М t . Разложение модуля М вида
называется каноническим разложением модуля М. Обозначим niMi=Li, так, что
Неприводимые подмодули модулей L i обозначим
; i=1, 2, …, t. (36)
Эти модули нам необходимо найти.
Предположим, что задача решена. Следовательно, в каждом из модмодулей M i (s) (s=1, 2, …, n i) найдена ортонормированная база, в которой оператор представлен матрицей Т i (g) неприводимого представления Т, полученного в результате действия (по правилу из § 3) оператора на базу по формуле

J=1, 2, …, m i . (37)
В этом выражении можно считать, что m i - размерность неприводимого представления T i (i=1, 2, …, t), причем - элементы базы с номером g из неприводимого подмодуля M i . Разместим теперь элементы базы L i при фиксированном i следующим образом:

Справа в выражении (38) расположены базы модулей M i (1) , M i (2) , …, . Если же i изменять от 1 до t, то получим искомую базу всего модуля М, состоящего из m 1 n 1 + m 2 n 2 +…+ m t n t элементов.
Рассмотрим теперь оператор

действующий в модуле М (j фиксировано). Согласно теореме 2, - оператор проектирования. Поэтому этот оператор оставляет без изменения все базисные элементы (s=1, 2, …, n i), расположенные в j-м столбце выражения (38), и обращает в нуль все остальные векторы базы. Обозначим через M ij векторное пространство, натянутое на ортогональную систему векторов, стоящие в j-м столбце выражения (38). Тогда можно сказать, что является оператором проектирования на пространство M ij . Оператор известен, так как известны диагональные элементы матриц неприводимых представлений групп, а также оператор T(g).
Теперь можно решить нашу задачу.
Выберем n i произвольных базисных векторов в M: и подействуем на них оператором проектирования. Полученные векторы лежат в пространстве M ij и являются линейно независимыми. Они не обязательно ортогональны и нормированы. Ортонормируем полученную систему векторов согласно правилу из § 2. Полученную систему векторов обозначим e ij (s) в соответствии с обозначениями, принятыми в предположении, что задача решена. Как уже обозначалось, здесь j фиксировано, а s=1, 2, …, n i . Обозначим e if (s) (f=1, 2, …, j-1, j+1, …, m i), остальные элементы базы модуля M i размерности n i m i . Обозначим через следующий оператор:

Из соотношений ортогональности для матриц неприводимых представлений следует, что этот оператор дает возможность получить e ig s по формуле
I=1, 2, …, t. (41)
Все сказанное можно выразить в виде следующего алгоритма.
Для того, чтобы найти базу модуля М из элементов, преобразующихся по неприводимым представлениям Т i , содержащихся в представлении Т, связанном с модулем М, необходимо:
По формуле (32) найти размерности подпространств М ij , соответствующих j-компоненте неприводимого представления T i .
Найти с помощью оператора проектирования (39) все подпространства M ij .
В каждом подпространстве M ij выбрать произвольную ортонормированную базу.
Используя формулу (41), найти все элементы базы, преобразующихся по остальным компонентам неприводимого представления Т i .





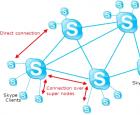 Смотреть что такое "VoIP" в других словарях Связь ip телефония
Смотреть что такое "VoIP" в других словарях Связь ip телефония Получение Root Fly IQ441 Radiance Прошивка андроид для fly iq441
Получение Root Fly IQ441 Radiance Прошивка андроид для fly iq441 Как разбить PDF файл на части
Как разбить PDF файл на части Скачать все файлы dll для windows 8
Скачать все файлы dll для windows 8